Wahrscheinlichkeitstheorie an Polyedern

Hallo.

Wie versprochen kommt jetzt etwas Stochastik. Ich gehe hier erstmal nur auf Würfel ein und setze voraus, dass jeder weiß, dass Wahrscheinlichkeiten als Zahl zwischen 0 und 1 angegeben werden und dass auf 1W6 die Wahrscheinlichkeit 5+ zu würfeln grade 1/3 ist.

Ich verzichte hier auf allen weiteren, mathematischen Hintergrund. Mit P(A) meine ich die Wahrscheinlichkeit des Ereignisses A, ohne jetzt Rücksicht darauf zu nehmen, in welcher Menge ich mich gerade befinde. Die Links sind jeweils Wikipedia.


Gegenereignisse
Wie hoch ist die Wahrscheinlichkeit auf einem W20 keine 17 zu würfeln? Das ist grade die Wahrscheinlichkeit irgendeine andere Zahl zu würfeln und davon gibts genau 19. Also: 19/20.

Das ist aber gerade 1 - 1/20 = 1 - P(19). Diese Regel gilt bei bei beliebigen Ereignissen. Die Wahrscheinlichkeit, dass ein Ereignis A nicht eintritt, ist also 1 - P(A).

Das ist z.B. nützlich um herauszufinden, wie hoch die Wahrscheinlichkeit ist, dass mindestens ein Würfel eine bestimmte Zahl x zeigt. Das ist nämlich genau das Gegenereignis zu "Kein Würfel zeigt x.".


"UND"-Ereignisse bei mehreren Würfelwürfen
Wie hoch ist die Wahrscheinlichkeit auf einem W10 eine 9 zu würfeln UND dann auf einem W8 noch eine 7? Wie hoch ist die Wahrscheinlichkeit auf 3W6 je eine 1 zu würfeln?

Diese Probleme lassen sich leicht beantworten, da verschiedene Würfel stochastisch unabhängig sind. Die Einzelwahrscheinlichkeiten werden in diesen Fällen einfach multipliziert. D.h.:

P("9 auf W10" UND "7 auf W8") = P("9 auf W10") * P("7 auf W8") = 1/10 * 1/8 = 1/80.

Für die Frage nach (1,1,1) auf 3W6 ergibt sich also gerade P("3 auf W6") * P("3 auf W6") * P("3 auf W6") = P("3 auf W6") ³ = (1/6) ³ = 1/216.


"ODER"-Ereignisse
Nu kennen wir das UND, brauchen wir noch das ODER. Einfach sind die Fälle wie "3 oder 5 auf W6". Das ist einfach 2/6. Das dies so ist, dass die Ereignisse "3 auf W6" und "5 auf W6" disjunkt sind. D.h. ein Würfel kann niemals gleichzeitig 3 und 5 zeigen.

Wir halten fest: Die Wahrscheinlichkeit von "A oder B" ist gleich P(A)+P(B), wenn A und B niemals gleichzeitig eintreten. (Das gilt auch, wenn A und B auf verschiedenen Würfeln oder überhaupt auf ganz anderen Prozessen basieren. Das gilt immer.)

Komplizierter wird es, wenn A und B nicht disjunkt sind. Betrachten wir das Ereignis "Eine 1 auf 2W2" = "1 auf W2₁" ODER "1 auf W2₂". Die Formel P(A)+P(B) ergibt hier 0,5 + 0,5 = 1. Es müsste also immer ein Würfel eine 1 zeigen. Das ist aber offenbar falsch. Das Ergebnis ist zu hoch.

Man kann diese beiden Ereignisse gut als Flächen darstellen und tatsächlich ist die Wahrscheinlichkeitstheorie eine Art angepasste Flächenmessung.



Wenn wir die Flächen der beiden Kreise addieren, so haben wir den Schnitt der beiden Kreise doppelt gemessen. Der Schnitt entspricht aber gerade der Wahrscheinlichkeit, dass Würfel₁ UND Würfel₂ eine 1 zeigen. Diese Wahrscheinlichkeit haben wir eben berechnet als 1/2 * 1/2 = 1/4.

Die endgültige Wahrscheinlichkeit für unser W2-Problem ist also 1/2 + 1/2 - 1/4 = 3/4. Das stimmt mit dem Lösungweg über das Gegenereignis (s.o.) überein.

Wenn man diese Methode auf die Verknüpfung mehrer Ereignisse erweitert erhält man die Siebformel.


Die Binomialverteilung
OK. Soweit wars einfach, jetzt kommen die harten Probleme, in Rollenspielkreisen besser bekannt als Poolsysteme.

Wie hoch ist die Wahrscheinlichkeit beim Werfen von 5W6 zweiWürfel zu erhalten, die 3+ zeigen? Offenbar braucht es hier drei Angaben:

• n := Die Gesamtzahl der geworfenen Würfel.
• k := Die Zahl der Würfel, die irgendetwas tun sollen. - Die Zahl der Erfolge.
  
• p := Die Wahrscheinlichkeit, dass einer von diesen k Würfeln das Gewünschte tut.

Für das obige Beispiel gilt also n=5 und k=2. Wie hoch ist die Wahrscheinlichkeit, dass 1W6 drei oder mehr zeigt? Klar, das ist 4/6 und das ist p. Die Wahrscheinlichkeit, dass ein bestimmter Würfel kein Erfolg ist wird häufig als q bezeichnet. D.h. q = 1 - p = 1 - 4 /6 = 2/6.

Nehmen wir mal an, die ersten zwei Würfel zeigen 3+. Dann müssen die übrigen 2- zeigen, damit es am Ende nicht mehr als zwei Erfolge sind. Wie hoch ist die Wahrscheinlichkeit für diese Kombination? Das ist nach der UND-Regel grade p * p * q * q *q = (4/6)² * (2/6)³ = p² * (1-p)³ = p^k * (1-p)^n-k. Die gleiche Wahrscheinlichkeit erhält man auch, wenn die Erfolg an zweiter und vierter Stelle oder sonstwo liegen.

Jetzt muss man eigentlich nur noch herausfinden, wie viele Kombinationen es gibt, die Erfolge auf die Würfel zu verteilen, und das ganze dann mit p^k * (1-p)^n-k multiplizieren. Die Antwort liefert der Binomialkoeffizient, der einigen wohl als Pascal'sches Dreieck bekannt sein sollte.

Wir erhalten also die sog. Binomialverteilung B(n,p,k) = n!/( (n-k)! k!) * p^k * (1-p)^n-k.


Summen von Würfeln
Die Wahrscheinlichkeiten, die sich aus der Summe oder Differenz mehrerer Würfel lassen sich als Formel darstellen. Allerdings ist die Formel (meines Erachtens) komplizierter als sich das jeweils kurz zu überlegen.

Wie für die Binomialverteilung überlegt man sich einfach wieder, wie hoch die Wahrscheinlichkeit ist, dass eine ganz bestimmte Kombination von Ergebnissen (mit festgelegter Reihenfolge) fällt. Wenn man nWx betrachtet - also n Würfel mit je x Seiten - ist das einfach (1/x)ⁿ.

Dann am besten alle anfallenden Kombinationen hinschreiben und zählen. Bei nur zwei Würfeln ist das ganze noch etwas einfacher. Die beiden extremsten Ergebnisse haben die Wahrscheinlichkeit 1 / x². Zum Mittelwert hin, gibt es jeweils eine Kombination mehr, also 2 / x², 3 / x² usw.


Explodierende Würfel
Müssen einfach Erwähnung finden, weil die Bezeichnung so toll ist. Damit ist gemeint, dass ein Würfel der sein maximales Ergebnis zeigt, noch einmal geworfen werden kann und das neue Ergebnis zum Alten dazu addiert wird.

Dieser Sonderfall ist eigentlich keiner. Die Wahrscheinlichkeit auf einem explodierenden W10 eine 8 zu werfen ist nach der UND-Regel 1/10 * 1/8 = 1/80.

Bei explodierenden Poolsystemen à la Shadowrun muss man also nur das p für Binomialverteilung passend berechnen.

Schwieriger wirds mit den Kollegen...

Generierende Würfel
Der Titel ist meine eigene Erfindung (ich fand ihn ganz passen zu explodierend) und es handelt sich um das Konzept von nWoD und ähnlichen Vertretern: Es werden n Würfel gewürfelt, die mit Wahrscheinlich p jeweils einen Erfolg geben und mit Wahrscheinlichkeit r einen Erfolg geben und einen weiteren Würfel produzieren, der sich ebenso verhält. (D.h.: r < p =" 0,3" r =" 0,1." href="http://grofafo.org/index.php/topic,27452.0.html">hier im Grofafo.)

Definiere W(k) als die Wahrscheinlichkeit mit einem Würfel k Erfolge zu erzielen. Dann gilt:

W(k) = r^k-1 * (1-r) * p

Für n Würfel muss man alle Wahrscheinlichkeiten summieren, dass sich die Würfel die k Erfolge unter einander aufteilen. Man erhält:







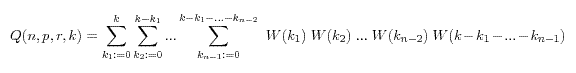
Die Multinomialverteilung
Die Multinomialverteilung ist die Verallgemeinerung der Binomialverteilung. Während es bei der Binomialverteilung nur zwei Ausgänge gibt - Erfolg und Misserfolg - sind bei der Multinomialverteilung verschieden viele Ausgänge möglich.

Man hat also wieder n Würfel und dann für jedes Ergebnis eine Wahrscheinlichkeit p₁, p₂, ..., p_t. Daneben werden noch Angaben benötigt, wie oft jedes Ergebnis jeweils auftreten soll. Die Formel gibts dann hier bei Wikipedia.

Um z.B. die Wahrscheinlichkeit für k Erfolge im oWoD auszurechnen, müsste man alle Kombinationen von -1, 0 und 1 mit Summe k aufschreiben, für jede mit Hilfe der 3-Multinomialverteilung die Wahrscheinlichkeit ausrechnen und das ganze addieren.



Das wars so weit von mir. Bei Fehlern meckern, bei Fragen fthagn. Und wer noch ein spezielles Problem nachgerechnet haben möchte, kann hier auch Bescheid sagen oder mich anschreiben. (7te See und DSA verweiger ich. Die sind mir zu kompliziert.)