Moin.
In Forgekreisen gibt es ein recht beliebtes Mittel namens Power19, einen Katalog von 19 Fragen, den ein Designer benutzen soll, um sich über sein Spiel klar zu werden. (Die Liste und einige Anmerkungen gibts auf Socrates RPG, einem Blog über Rollenspieldesign, den ich leider über weite Strecken ziemlich unbrauchbar finde.)
Ich persönlich finde die Power19 aus verschiedenen Gründen schlecht. Erstens kann sich niemand den ganzen Katalog merken, zweitens wird Hintergrund nicht gleichberechtigt zu Spielstil und Core Story, drittens sind the Power19 deduktiv und die meisten Leute, kommen mit Frage 1 einfach nicht klar.
Daher gibts hier meinen, persönlichen Katalog. Und weil Englisch so ungemein cool ist, gibts die natürlich in Englisch.
1. What do you imagine the players to do? Are there different roles and responsibilities? If so, which?
2. What do you imagine the protagonists to do?
3. How do you imagine the settting?
4. Which of these answers do you consider most important and which do you plan to present in your book?
5. Who shall play the game where and when?
6. How long does it take to play the game? How is it structured?
7. Which rules have you derived from answers 1 - 6?
8. Finally, summarize what your games is about.
Sonntag, Juli 16, 2006
Dienstag, Juli 04, 2006
Resolution
Moin.
Heute gehts, um die wohl best erforschten Techniken im Rollenspiel. Meine persönliche Auffassung dazu, welche es denn sonst gibt, findet sich nach wie vor hier.
In meiner Einteilung habe ich ja Resolution als Änderung des Vorstellungsraums beschrieben. Um genauer zu sein, müsste man vielleicht von absichtsvollen Veränderungen, während des laufenden Spiels sprechen.
Denn es kommt ja z.B. vor, dass die Vorstellung etwa durch die Wahl von Hintergrund und Genre quasi präfiguriert wird oder dass sich der Vorstellungsraum während des Spiels ungewollt verändert, etwa wenn die Teilnehmer Fakten vergessen. Beides würde mit dem gängigen Resolutionsbegriff nicht übereinstimmen. (Es gibt auch Leute, die schränken den Begriff noch weiter ein. Das soll mich aber nicht kümmern.)
Wie mir inzwischen aufgefallen ist, war ich allerdings etwas inkonsequent. Ich habe ja aufgezeigt, dass Rollenspiel häufig zwei Spielplätze hat: Vorstellung und Werte. Insofern sind eigentlich auch die Änderungen an beiden Stellen interessant, so dass man quasi an zwei Stellen Resolution betreiben kann. Ich spreche daher von nun an von Resolution und W-Resolution.
Häufig sind diese Vorgänge natürlich stark vermischt, was wohl der Grund ist, dass ich niemanden kenne, der sie so auseinandergepflückt hat.
DKF
Vorweg allerdings ein wenig Historie. Die vermutlich erste Einteilung von Resolutionstechniken stammt von Jonathan Tweet und findet sich in Everway. Ich tu jetzt etwas ganz böses und zitiere aus zweiter Hand, nämlich aus dem Aufsatz "System does matter" von Ron Edwards. (Das ist übrigens der Ursprung von Gulasch, Nudeln und Salat.)
Demnach gibt es drei Typen von Resolution:
Informationsquellen
Kaum beachtet dagegen wird die Frage, was denn da eingebracht wird bzw. woher die neue Information stammt. Da gibt es eigentlich nur zwei Möglichkeiten: Von den Spielern oder aus der Mechanik.
Wenn ein Mechanismus selbst gewisse Informationen liefert, habe ich teilweise schon gehört, dass er informativ sei. Ich übernehme diese Bezeichnung mal.
Wenn die Information von den Spielern stammt, lassen sich zwei Varianten feststellen. Entweder ein Teilnehmer ist ermächtigt, bestimmte Informationen einzubringen, oder die Informationen wurden verhandelt und von mehreren Teilnehmern zusammen hervorgebracht. (Ich benutze die Bezeichnung "ermächtigt" analog zu dem Begriff "Player Empowerment", der von einigen Leuten benutzt wird.)
Ich nehme mir mal ein Beispiel eines Resolutionsprozesses her (Agone, p. 168):
Diese Kampftechnik ist informativ in Bezug auf die Vorstellung (8-förmiger Schwung der Axt, der alle Gegner trifft) und in Bezug auf die Werte (Schaden an allen Gegnern). Man sieht hier sehr schön, dass V-Resolution und W-Resolution zusammen auftreten können.
Natürlich kann ein Charakter bei Agone auch einen Angriff machen, ohne eine Spezialtechnik zu benutzen. So ein Angriff ist natürlich auch sehr informativ in Hinsicht auf die Werte, allerdings deutlich weniger in Hinsicht auf die Fiktion. Es findet sich im Buch auch nichts über erzählerische Ausschmückung seitens eines Teilnehmers, obwohl dies wahrscheinlich passieren wird. Tatsächlich können wir wohl davon ausgehen, dass in den meisten Agone-Runden der kontrollierende Spieler mit einer impliziten Regel ermächtigt wird, Ausschmückungen vorzunehmen.
Man sieht also schon, dass beide Ebenen und verschiedene Informationsquellen in einer Resolution zusammenkommen können.
Stake Resolution
Tatsächlich gibt es noch eine weitere Quelle bzw. eine Kombination aus verhandelter und informativer Resolution, die sich insbesondere bei Spielen aus dem Dunstkreis der Forge (und damit auch bei mir) großer Beliebtheit erfreut. Hier wird zuerst in der Gruppe über mögliche Ausgänge eines Problems entschieden und mit Hilfe von bestimmten Mechanismen entschieden, welches Ergebnis schließlich eintritt. Die möglichen Ausgänge werden häufig als Stakes (Einsätze) bezeichnet. Daher schließe ich mich denen an, die diese Variante als Stake Resolution bezeichnen.
Tatsächlich kommt Stake Resolution in vielen Spielrunden vor. Häufig in der Form: "Würfel mal. Wenn du schaffst, kriegst du die Tür auf, wenn du's nicht schaffst, nicht." Auch hier wird eine Vorauswahl über mögliche Ergebnisse verhandelt und dann per Fortune-Mechanik entschieden. (Ja, wenn der Spielleiter sowas sagt ist das eine Verhandlung bzw. die Äußerung ein Verhandlungsangebot. So spricht Mr. Baker und so will ich das glauben. Siehe auch den Grundlagen-Artikel.)
Georgios hat im Grofafo neulich ein Thema zu verschiedenen Arten von Stakes gestartet. Lesenswert.
Conflict Resolution & Task Resolution
Wo ich schon dabei bin, will ich auch auf zwei weitere Gummibandbegriffe aus der Forge hinweisen: Conflict Resolution und Task Resolution. Das Folgende sind die Definitionen aus dem Provisional Glossary:
Theoretisch kann man damit also arbeiten. Tatsächlich setzen aber viele Sprecher Conflict Resolution mit Stake Resolution gleich oder interpretieren in die CR zumindest die Bekanntheit aller möglichen Ausgänge hinein. Da ist also Vorsicht geboten. Insbesondere deshalb, weil einige Leute wieder die Forge-Krankheit überfällt und sie daher meinen, dass es nur CR und TR gebe und nichts anderes. Tatsächlich ist Resolution aber ein deutlich komplexeres Thema, wie wir hier gesehen haben.
Nochmal zum Abschluss: Resolutionsprozesse sind komplexe Gebilde die mindestens nach den folgenden Gesichtspunkten betrachtet werden können:
Tipps
Kommen wir zu Design-Ratschlägen, denn dazu sind wir ja eigentlich hier. Da kann ich leider gar nicht soo viel zu sagen.
Grundsätzlich ist der Vorteil bei informativen Mechanismen, dass unvorhergesehenes passieren kann (zumindest in dem Rahmen, den der Mechanismus umfasst). Dagegen gibt es insbesondere bei den Varianten, die Verhandlung beinhalten, die Möglichkeit unpassende Ergebnisse von vornherein auszufiltern. Beides kann in bestimmten Situationen interessant sein.
Weiter gilt, dass viele sich mehr dafür interessieren, worauf sie Einfluss haben. (Sieht man schön, wenn Spieler anfangen irgendwas zu lesen, wenn sie nicht dran sind.) Insofern haben Prozeduren, die möglichst viele Teilnehmer beteiligen einen gewissen Vorteil, können aber natürlich auch anstregender sein, wenn alle immer etwas tun müssen. - Die Erfahrung hab ich zumindest mit einigen Forge-Spielen gemacht.
Problematisch kann es sein, nicht genau zu sagen, was aus welcher Quelle stammt. Das führt häufig zu Interpretationsproblemen und sollte meines Erachtens vermieden werden.
Zuletzt bin ich ja - wie ich auch hier schön häufiger angemerkt habe - abgeneigt, einen beliebigen Teilnehmer zu ermächtigen, Dinge auf der W-Ebene frei nach Schnauze zu ändern.
Heute gehts, um die wohl best erforschten Techniken im Rollenspiel. Meine persönliche Auffassung dazu, welche es denn sonst gibt, findet sich nach wie vor hier.
In meiner Einteilung habe ich ja Resolution als Änderung des Vorstellungsraums beschrieben. Um genauer zu sein, müsste man vielleicht von absichtsvollen Veränderungen, während des laufenden Spiels sprechen.
Denn es kommt ja z.B. vor, dass die Vorstellung etwa durch die Wahl von Hintergrund und Genre quasi präfiguriert wird oder dass sich der Vorstellungsraum während des Spiels ungewollt verändert, etwa wenn die Teilnehmer Fakten vergessen. Beides würde mit dem gängigen Resolutionsbegriff nicht übereinstimmen. (Es gibt auch Leute, die schränken den Begriff noch weiter ein. Das soll mich aber nicht kümmern.)
Wie mir inzwischen aufgefallen ist, war ich allerdings etwas inkonsequent. Ich habe ja aufgezeigt, dass Rollenspiel häufig zwei Spielplätze hat: Vorstellung und Werte. Insofern sind eigentlich auch die Änderungen an beiden Stellen interessant, so dass man quasi an zwei Stellen Resolution betreiben kann. Ich spreche daher von nun an von Resolution und W-Resolution.
Häufig sind diese Vorgänge natürlich stark vermischt, was wohl der Grund ist, dass ich niemanden kenne, der sie so auseinandergepflückt hat.
DKF
Vorweg allerdings ein wenig Historie. Die vermutlich erste Einteilung von Resolutionstechniken stammt von Jonathan Tweet und findet sich in Everway. Ich tu jetzt etwas ganz böses und zitiere aus zweiter Hand, nämlich aus dem Aufsatz "System does matter" von Ron Edwards. (Das ist übrigens der Ursprung von Gulasch, Nudeln und Salat.)
Demnach gibt es drei Typen von Resolution:
-
Fortune, meaning a range of results is possible for each instance (I rolled a 10 on 3 dice, under my skill of 12; I hit!). Most RPG systems are primarily Fortune-based for historical reasons; methods include dice, cards, and all sorts of other things.
-
Karma, which compares two fixed values (I have a 7 in fencing, you have a 4, I win). Amber is one of the few mainly-Karma games.
-
Drama, in which the GM (or rarely, the player) resolves the outcome by saying what happens ("You skewer him!" says the GM, without rolling or consulting numbers of any kind).
Informationsquellen
Kaum beachtet dagegen wird die Frage, was denn da eingebracht wird bzw. woher die neue Information stammt. Da gibt es eigentlich nur zwei Möglichkeiten: Von den Spielern oder aus der Mechanik.
Wenn ein Mechanismus selbst gewisse Informationen liefert, habe ich teilweise schon gehört, dass er informativ sei. Ich übernehme diese Bezeichnung mal.
Wenn die Information von den Spielern stammt, lassen sich zwei Varianten feststellen. Entweder ein Teilnehmer ist ermächtigt, bestimmte Informationen einzubringen, oder die Informationen wurden verhandelt und von mehreren Teilnehmern zusammen hervorgebracht. (Ich benutze die Bezeichnung "ermächtigt" analog zu dem Begriff "Player Empowerment", der von einigen Leuten benutzt wird.)
Ich nehme mir mal ein Beispiel eines Resolutionsprozesses her (Agone, p. 168):
Double Phoenix (Action) [Double Axe, 24]
Requirement: fighting at least two opponents, whose SIZ is inferior to the attacker's
The attack inflicts as much damage to all opponents as it does to the target of the blow ( the opponent that parries). The movement of the axe resembles the shape of an eight is gnerally very bloody.
Diese Kampftechnik ist informativ in Bezug auf die Vorstellung (8-förmiger Schwung der Axt, der alle Gegner trifft) und in Bezug auf die Werte (Schaden an allen Gegnern). Man sieht hier sehr schön, dass V-Resolution und W-Resolution zusammen auftreten können.
Natürlich kann ein Charakter bei Agone auch einen Angriff machen, ohne eine Spezialtechnik zu benutzen. So ein Angriff ist natürlich auch sehr informativ in Hinsicht auf die Werte, allerdings deutlich weniger in Hinsicht auf die Fiktion. Es findet sich im Buch auch nichts über erzählerische Ausschmückung seitens eines Teilnehmers, obwohl dies wahrscheinlich passieren wird. Tatsächlich können wir wohl davon ausgehen, dass in den meisten Agone-Runden der kontrollierende Spieler mit einer impliziten Regel ermächtigt wird, Ausschmückungen vorzunehmen.
Man sieht also schon, dass beide Ebenen und verschiedene Informationsquellen in einer Resolution zusammenkommen können.
Stake Resolution
Tatsächlich gibt es noch eine weitere Quelle bzw. eine Kombination aus verhandelter und informativer Resolution, die sich insbesondere bei Spielen aus dem Dunstkreis der Forge (und damit auch bei mir) großer Beliebtheit erfreut. Hier wird zuerst in der Gruppe über mögliche Ausgänge eines Problems entschieden und mit Hilfe von bestimmten Mechanismen entschieden, welches Ergebnis schließlich eintritt. Die möglichen Ausgänge werden häufig als Stakes (Einsätze) bezeichnet. Daher schließe ich mich denen an, die diese Variante als Stake Resolution bezeichnen.
Tatsächlich kommt Stake Resolution in vielen Spielrunden vor. Häufig in der Form: "Würfel mal. Wenn du schaffst, kriegst du die Tür auf, wenn du's nicht schaffst, nicht." Auch hier wird eine Vorauswahl über mögliche Ergebnisse verhandelt und dann per Fortune-Mechanik entschieden. (Ja, wenn der Spielleiter sowas sagt ist das eine Verhandlung bzw. die Äußerung ein Verhandlungsangebot. So spricht Mr. Baker und so will ich das glauben. Siehe auch den Grundlagen-Artikel.)
Georgios hat im Grofafo neulich ein Thema zu verschiedenen Arten von Stakes gestartet. Lesenswert.
Conflict Resolution & Task Resolution
Wo ich schon dabei bin, will ich auch auf zwei weitere Gummibandbegriffe aus der Forge hinweisen: Conflict Resolution und Task Resolution. Das Folgende sind die Definitionen aus dem Provisional Glossary:
- Conflict resolution: A Technique in which the mechanisms of play focus on conflicts of interest, rather than on the component tasks within that conflict. When using this Technique, inanimate objects are conceived to have "interests" at odds with the character, if necessary. Contrast with Task resolution.
- Task resolution: A Technique in which the Resolution mechanisms of play focus on within-game cause, in linear in-game time, in terms of whether the acting character is competent to perform a task. Contrast with Conflict resolution.
Theoretisch kann man damit also arbeiten. Tatsächlich setzen aber viele Sprecher Conflict Resolution mit Stake Resolution gleich oder interpretieren in die CR zumindest die Bekanntheit aller möglichen Ausgänge hinein. Da ist also Vorsicht geboten. Insbesondere deshalb, weil einige Leute wieder die Forge-Krankheit überfällt und sie daher meinen, dass es nur CR und TR gebe und nichts anderes. Tatsächlich ist Resolution aber ein deutlich komplexeres Thema, wie wir hier gesehen haben.
Nochmal zum Abschluss: Resolutionsprozesse sind komplexe Gebilde die mindestens nach den folgenden Gesichtspunkten betrachtet werden können:
- Ebenen: V-Resolution, W-Resolution
- Quellen: Informativ, Ermächtigend, Verhandelt, Stake Resolution, vielleicht weitere.
- Mittel: Drama, Karma, Fortune, Skill, vermutlich weitere.
Tipps
Kommen wir zu Design-Ratschlägen, denn dazu sind wir ja eigentlich hier. Da kann ich leider gar nicht soo viel zu sagen.
Grundsätzlich ist der Vorteil bei informativen Mechanismen, dass unvorhergesehenes passieren kann (zumindest in dem Rahmen, den der Mechanismus umfasst). Dagegen gibt es insbesondere bei den Varianten, die Verhandlung beinhalten, die Möglichkeit unpassende Ergebnisse von vornherein auszufiltern. Beides kann in bestimmten Situationen interessant sein.
Weiter gilt, dass viele sich mehr dafür interessieren, worauf sie Einfluss haben. (Sieht man schön, wenn Spieler anfangen irgendwas zu lesen, wenn sie nicht dran sind.) Insofern haben Prozeduren, die möglichst viele Teilnehmer beteiligen einen gewissen Vorteil, können aber natürlich auch anstregender sein, wenn alle immer etwas tun müssen. - Die Erfahrung hab ich zumindest mit einigen Forge-Spielen gemacht.
Problematisch kann es sein, nicht genau zu sagen, was aus welcher Quelle stammt. Das führt häufig zu Interpretationsproblemen und sollte meines Erachtens vermieden werden.
Zuletzt bin ich ja - wie ich auch hier schön häufiger angemerkt habe - abgeneigt, einen beliebigen Teilnehmer zu ermächtigen, Dinge auf der W-Ebene frei nach Schnauze zu ändern.
Montag, Juli 03, 2006
Wahrscheinlichkeitstheorie an Polyedern
Hallo.
Wie versprochen kommt jetzt etwas Stochastik. Ich gehe hier erstmal nur auf Würfel ein und setze voraus, dass jeder weiß, dass Wahrscheinlichkeiten als Zahl zwischen 0 und 1 angegeben werden und dass auf 1W6 die Wahrscheinlichkeit 5+ zu würfeln grade 1/3 ist.
Ich verzichte hier auf allen weiteren, mathematischen Hintergrund. Mit P(A) meine ich die Wahrscheinlichkeit des Ereignisses A, ohne jetzt Rücksicht darauf zu nehmen, in welcher Menge ich mich gerade befinde. Die Links sind jeweils Wikipedia.
Gegenereignisse
Wie hoch ist die Wahrscheinlichkeit auf einem W20 keine 17 zu würfeln? Das ist grade die Wahrscheinlichkeit irgendeine andere Zahl zu würfeln und davon gibts genau 19. Also: 19/20.
Das ist aber gerade 1 - 1/20 = 1 - P(19). Diese Regel gilt bei bei beliebigen Ereignissen. Die Wahrscheinlichkeit, dass ein Ereignis A nicht eintritt, ist also 1 - P(A).
Das ist z.B. nützlich um herauszufinden, wie hoch die Wahrscheinlichkeit ist, dass mindestens ein Würfel eine bestimmte Zahl x zeigt. Das ist nämlich genau das Gegenereignis zu "Kein Würfel zeigt x.".
"UND"-Ereignisse bei mehreren Würfelwürfen
Wie hoch ist die Wahrscheinlichkeit auf einem W10 eine 9 zu würfeln UND dann auf einem W8 noch eine 7? Wie hoch ist die Wahrscheinlichkeit auf 3W6 je eine 1 zu würfeln?
Diese Probleme lassen sich leicht beantworten, da verschiedene Würfel stochastisch unabhängig sind. Die Einzelwahrscheinlichkeiten werden in diesen Fällen einfach multipliziert. D.h.:
P("9 auf W10" UND "7 auf W8") = P("9 auf W10") * P("7 auf W8") = 1/10 * 1/8 = 1/80.
Für die Frage nach (1,1,1) auf 3W6 ergibt sich also gerade P("3 auf W6") * P("3 auf W6") * P("3 auf W6") = P("3 auf W6") ³ = (1/6) ³ = 1/216.
"ODER"-Ereignisse
Nu kennen wir das UND, brauchen wir noch das ODER. Einfach sind die Fälle wie "3 oder 5 auf W6". Das ist einfach 2/6. Das dies so ist, dass die Ereignisse "3 auf W6" und "5 auf W6" disjunkt sind. D.h. ein Würfel kann niemals gleichzeitig 3 und 5 zeigen.
Wir halten fest: Die Wahrscheinlichkeit von "A oder B" ist gleich P(A)+P(B), wenn A und B niemals gleichzeitig eintreten. (Das gilt auch, wenn A und B auf verschiedenen Würfeln oder überhaupt auf ganz anderen Prozessen basieren. Das gilt immer.)
Komplizierter wird es, wenn A und B nicht disjunkt sind. Betrachten wir das Ereignis "Eine 1 auf 2W2" = "1 auf W21" ODER "1 auf W22". Die Formel P(A)+P(B) ergibt hier 0,5 + 0,5 = 1. Es müsste also immer ein Würfel eine 1 zeigen. Das ist aber offenbar falsch. Das Ergebnis ist zu hoch.
Man kann diese beiden Ereignisse gut als Flächen darstellen und tatsächlich ist die Wahrscheinlichkeitstheorie eine Art angepasste Flächenmessung.
Wenn wir die Flächen der beiden Kreise addieren, so haben wir den Schnitt der beiden Kreise doppelt gemessen. Der Schnitt entspricht aber gerade der Wahrscheinlichkeit, dass Würfel1 UND Würfel2 eine 1 zeigen. Diese Wahrscheinlichkeit haben wir eben berechnet als 1/2 * 1/2 = 1/4.
Die endgültige Wahrscheinlichkeit für unser W2-Problem ist also 1/2 + 1/2 - 1/4 = 3/4. Das stimmt mit dem Lösungweg über das Gegenereignis (s.o.) überein.
Wenn man diese Methode auf die Verknüpfung mehrer Ereignisse erweitert erhält man die Siebformel.
Die Binomialverteilung
OK. Soweit wars einfach, jetzt kommen die harten Probleme, in Rollenspielkreisen besser bekannt als Poolsysteme.
Wie hoch ist die Wahrscheinlichkeit beim Werfen von 5W6 zweiWürfel zu erhalten, die 3+ zeigen? Offenbar braucht es hier drei Angaben:
Nehmen wir mal an, die ersten zwei Würfel zeigen 3+. Dann müssen die übrigen 2- zeigen, damit es am Ende nicht mehr als zwei Erfolge sind. Wie hoch ist die Wahrscheinlichkeit für diese Kombination? Das ist nach der UND-Regel grade p * p * q * q *q = (4/6)² * (2/6)³ = p² * (1-p)³ = pk * (1-p)n-k. Die gleiche Wahrscheinlichkeit erhält man auch, wenn die Erfolg an zweiter und vierter Stelle oder sonstwo liegen.
Jetzt muss man eigentlich nur noch herausfinden, wie viele Kombinationen es gibt, die Erfolge auf die Würfel zu verteilen, und das ganze dann mit pk * (1-p)n-k multiplizieren. Die Antwort liefert der Binomialkoeffizient, der einigen wohl als Pascal'sches Dreieck bekannt sein sollte.
Wir erhalten also die sog. Binomialverteilung B(n,p,k) = n!/( (n-k)! k!) * pk * (1-p)n-k.
Summen von Würfeln
Die Wahrscheinlichkeiten, die sich aus der Summe oder Differenz mehrerer Würfel lassen sich als Formel darstellen. Allerdings ist die Formel (meines Erachtens) komplizierter als sich das jeweils kurz zu überlegen.
Wie für die Binomialverteilung überlegt man sich einfach wieder, wie hoch die Wahrscheinlichkeit ist, dass eine ganz bestimmte Kombination von Ergebnissen (mit festgelegter Reihenfolge) fällt. Wenn man nWx betrachtet - also n Würfel mit je x Seiten - ist das einfach (1/x)n.
Dann am besten alle anfallenden Kombinationen hinschreiben und zählen. Bei nur zwei Würfeln ist das ganze noch etwas einfacher. Die beiden extremsten Ergebnisse haben die Wahrscheinlichkeit 1 / x2. Zum Mittelwert hin, gibt es jeweils eine Kombination mehr, also 2 / x2, 3 / x2 usw.
Explodierende Würfel
Müssen einfach Erwähnung finden, weil die Bezeichnung so toll ist. Damit ist gemeint, dass ein Würfel der sein maximales Ergebnis zeigt, noch einmal geworfen werden kann und das neue Ergebnis zum Alten dazu addiert wird.
Dieser Sonderfall ist eigentlich keiner. Die Wahrscheinlichkeit auf einem explodierenden W10 eine 8 zu werfen ist nach der UND-Regel 1/10 * 1/8 = 1/80.
Bei explodierenden Poolsystemen à la Shadowrun muss man also nur das p für Binomialverteilung passend berechnen.
Schwieriger wirds mit den Kollegen...
Generierende Würfel
Der Titel ist meine eigene Erfindung (ich fand ihn ganz passen zu explodierend) und es handelt sich um das Konzept von nWoD und ähnlichen Vertretern: Es werden n Würfel gewürfelt, die mit Wahrscheinlich p jeweils einen Erfolg geben und mit Wahrscheinlichkeit r einen Erfolg geben und einen weiteren Würfel produzieren, der sich ebenso verhält. (D.h.: r < p =" 0,3" r =" 0,1." href="http://grofafo.org/index.php/topic,27452.0.html">hier im Grofafo.)
Definiere W(k) als die Wahrscheinlichkeit mit einem Würfel k Erfolge zu erzielen. Dann gilt:
Für n Würfel muss man alle Wahrscheinlichkeiten summieren, dass sich die Würfel die k Erfolge unter einander aufteilen. Man erhält:
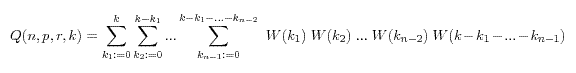
Die Multinomialverteilung
Die Multinomialverteilung ist die Verallgemeinerung der Binomialverteilung. Während es bei der Binomialverteilung nur zwei Ausgänge gibt - Erfolg und Misserfolg - sind bei der Multinomialverteilung verschieden viele Ausgänge möglich.
Man hat also wieder n Würfel und dann für jedes Ergebnis eine Wahrscheinlichkeit p1, p2, ..., pt. Daneben werden noch Angaben benötigt, wie oft jedes Ergebnis jeweils auftreten soll. Die Formel gibts dann hier bei Wikipedia.
Um z.B. die Wahrscheinlichkeit für k Erfolge im oWoD auszurechnen, müsste man alle Kombinationen von -1, 0 und 1 mit Summe k aufschreiben, für jede mit Hilfe der 3-Multinomialverteilung die Wahrscheinlichkeit ausrechnen und das ganze addieren.
Das wars so weit von mir. Bei Fehlern meckern, bei Fragen fthagn. Und wer noch ein spezielles Problem nachgerechnet haben möchte, kann hier auch Bescheid sagen oder mich anschreiben. (7te See und DSA verweiger ich. Die sind mir zu kompliziert.)
Wie versprochen kommt jetzt etwas Stochastik. Ich gehe hier erstmal nur auf Würfel ein und setze voraus, dass jeder weiß, dass Wahrscheinlichkeiten als Zahl zwischen 0 und 1 angegeben werden und dass auf 1W6 die Wahrscheinlichkeit 5+ zu würfeln grade 1/3 ist.
Ich verzichte hier auf allen weiteren, mathematischen Hintergrund. Mit P(A) meine ich die Wahrscheinlichkeit des Ereignisses A, ohne jetzt Rücksicht darauf zu nehmen, in welcher Menge ich mich gerade befinde. Die Links sind jeweils Wikipedia.
Gegenereignisse
Wie hoch ist die Wahrscheinlichkeit auf einem W20 keine 17 zu würfeln? Das ist grade die Wahrscheinlichkeit irgendeine andere Zahl zu würfeln und davon gibts genau 19. Also: 19/20.
Das ist aber gerade 1 - 1/20 = 1 - P(19). Diese Regel gilt bei bei beliebigen Ereignissen. Die Wahrscheinlichkeit, dass ein Ereignis A nicht eintritt, ist also 1 - P(A).
Das ist z.B. nützlich um herauszufinden, wie hoch die Wahrscheinlichkeit ist, dass mindestens ein Würfel eine bestimmte Zahl x zeigt. Das ist nämlich genau das Gegenereignis zu "Kein Würfel zeigt x.".
"UND"-Ereignisse bei mehreren Würfelwürfen
Wie hoch ist die Wahrscheinlichkeit auf einem W10 eine 9 zu würfeln UND dann auf einem W8 noch eine 7? Wie hoch ist die Wahrscheinlichkeit auf 3W6 je eine 1 zu würfeln?
Diese Probleme lassen sich leicht beantworten, da verschiedene Würfel stochastisch unabhängig sind. Die Einzelwahrscheinlichkeiten werden in diesen Fällen einfach multipliziert. D.h.:
P("9 auf W10" UND "7 auf W8") = P("9 auf W10") * P("7 auf W8") = 1/10 * 1/8 = 1/80.
Für die Frage nach (1,1,1) auf 3W6 ergibt sich also gerade P("3 auf W6") * P("3 auf W6") * P("3 auf W6") = P("3 auf W6") ³ = (1/6) ³ = 1/216.
"ODER"-Ereignisse
Nu kennen wir das UND, brauchen wir noch das ODER. Einfach sind die Fälle wie "3 oder 5 auf W6". Das ist einfach 2/6. Das dies so ist, dass die Ereignisse "3 auf W6" und "5 auf W6" disjunkt sind. D.h. ein Würfel kann niemals gleichzeitig 3 und 5 zeigen.
Wir halten fest: Die Wahrscheinlichkeit von "A oder B" ist gleich P(A)+P(B), wenn A und B niemals gleichzeitig eintreten. (Das gilt auch, wenn A und B auf verschiedenen Würfeln oder überhaupt auf ganz anderen Prozessen basieren. Das gilt immer.)
Komplizierter wird es, wenn A und B nicht disjunkt sind. Betrachten wir das Ereignis "Eine 1 auf 2W2" = "1 auf W21" ODER "1 auf W22". Die Formel P(A)+P(B) ergibt hier 0,5 + 0,5 = 1. Es müsste also immer ein Würfel eine 1 zeigen. Das ist aber offenbar falsch. Das Ergebnis ist zu hoch.
Man kann diese beiden Ereignisse gut als Flächen darstellen und tatsächlich ist die Wahrscheinlichkeitstheorie eine Art angepasste Flächenmessung.
Wenn wir die Flächen der beiden Kreise addieren, so haben wir den Schnitt der beiden Kreise doppelt gemessen. Der Schnitt entspricht aber gerade der Wahrscheinlichkeit, dass Würfel1 UND Würfel2 eine 1 zeigen. Diese Wahrscheinlichkeit haben wir eben berechnet als 1/2 * 1/2 = 1/4.
Die endgültige Wahrscheinlichkeit für unser W2-Problem ist also 1/2 + 1/2 - 1/4 = 3/4. Das stimmt mit dem Lösungweg über das Gegenereignis (s.o.) überein.
Wenn man diese Methode auf die Verknüpfung mehrer Ereignisse erweitert erhält man die Siebformel.
Die Binomialverteilung
OK. Soweit wars einfach, jetzt kommen die harten Probleme, in Rollenspielkreisen besser bekannt als Poolsysteme.
Wie hoch ist die Wahrscheinlichkeit beim Werfen von 5W6 zweiWürfel zu erhalten, die 3+ zeigen? Offenbar braucht es hier drei Angaben:
- n := Die Gesamtzahl der geworfenen Würfel.
- k := Die Zahl der Würfel, die irgendetwas tun sollen. - Die Zahl der Erfolge.
- p := Die Wahrscheinlichkeit, dass einer von diesen k Würfeln das Gewünschte tut.
Nehmen wir mal an, die ersten zwei Würfel zeigen 3+. Dann müssen die übrigen 2- zeigen, damit es am Ende nicht mehr als zwei Erfolge sind. Wie hoch ist die Wahrscheinlichkeit für diese Kombination? Das ist nach der UND-Regel grade p * p * q * q *q = (4/6)² * (2/6)³ = p² * (1-p)³ = pk * (1-p)n-k. Die gleiche Wahrscheinlichkeit erhält man auch, wenn die Erfolg an zweiter und vierter Stelle oder sonstwo liegen.
Jetzt muss man eigentlich nur noch herausfinden, wie viele Kombinationen es gibt, die Erfolge auf die Würfel zu verteilen, und das ganze dann mit pk * (1-p)n-k multiplizieren. Die Antwort liefert der Binomialkoeffizient, der einigen wohl als Pascal'sches Dreieck bekannt sein sollte.
Wir erhalten also die sog. Binomialverteilung B(n,p,k) = n!/( (n-k)! k!) * pk * (1-p)n-k.
Summen von Würfeln
Die Wahrscheinlichkeiten, die sich aus der Summe oder Differenz mehrerer Würfel lassen sich als Formel darstellen. Allerdings ist die Formel (meines Erachtens) komplizierter als sich das jeweils kurz zu überlegen.
Wie für die Binomialverteilung überlegt man sich einfach wieder, wie hoch die Wahrscheinlichkeit ist, dass eine ganz bestimmte Kombination von Ergebnissen (mit festgelegter Reihenfolge) fällt. Wenn man nWx betrachtet - also n Würfel mit je x Seiten - ist das einfach (1/x)n.
Dann am besten alle anfallenden Kombinationen hinschreiben und zählen. Bei nur zwei Würfeln ist das ganze noch etwas einfacher. Die beiden extremsten Ergebnisse haben die Wahrscheinlichkeit 1 / x2. Zum Mittelwert hin, gibt es jeweils eine Kombination mehr, also 2 / x2, 3 / x2 usw.
Explodierende Würfel
Müssen einfach Erwähnung finden, weil die Bezeichnung so toll ist. Damit ist gemeint, dass ein Würfel der sein maximales Ergebnis zeigt, noch einmal geworfen werden kann und das neue Ergebnis zum Alten dazu addiert wird.
Dieser Sonderfall ist eigentlich keiner. Die Wahrscheinlichkeit auf einem explodierenden W10 eine 8 zu werfen ist nach der UND-Regel 1/10 * 1/8 = 1/80.
Bei explodierenden Poolsystemen à la Shadowrun muss man also nur das p für Binomialverteilung passend berechnen.
Schwieriger wirds mit den Kollegen...
Generierende Würfel
Der Titel ist meine eigene Erfindung (ich fand ihn ganz passen zu explodierend) und es handelt sich um das Konzept von nWoD und ähnlichen Vertretern: Es werden n Würfel gewürfelt, die mit Wahrscheinlich p jeweils einen Erfolg geben und mit Wahrscheinlichkeit r einen Erfolg geben und einen weiteren Würfel produzieren, der sich ebenso verhält. (D.h.: r < p =" 0,3" r =" 0,1." href="http://grofafo.org/index.php/topic,27452.0.html">hier im Grofafo.)
Definiere W(k) als die Wahrscheinlichkeit mit einem Würfel k Erfolge zu erzielen. Dann gilt:
W(k) = rk-1 * (1-r) * p
Für n Würfel muss man alle Wahrscheinlichkeiten summieren, dass sich die Würfel die k Erfolge unter einander aufteilen. Man erhält:
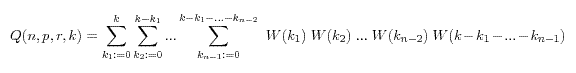
Die Multinomialverteilung
Die Multinomialverteilung ist die Verallgemeinerung der Binomialverteilung. Während es bei der Binomialverteilung nur zwei Ausgänge gibt - Erfolg und Misserfolg - sind bei der Multinomialverteilung verschieden viele Ausgänge möglich.
Man hat also wieder n Würfel und dann für jedes Ergebnis eine Wahrscheinlichkeit p1, p2, ..., pt. Daneben werden noch Angaben benötigt, wie oft jedes Ergebnis jeweils auftreten soll. Die Formel gibts dann hier bei Wikipedia.
Um z.B. die Wahrscheinlichkeit für k Erfolge im oWoD auszurechnen, müsste man alle Kombinationen von -1, 0 und 1 mit Summe k aufschreiben, für jede mit Hilfe der 3-Multinomialverteilung die Wahrscheinlichkeit ausrechnen und das ganze addieren.
Das wars so weit von mir. Bei Fehlern meckern, bei Fragen fthagn. Und wer noch ein spezielles Problem nachgerechnet haben möchte, kann hier auch Bescheid sagen oder mich anschreiben. (7te See und DSA verweiger ich. Die sind mir zu kompliziert.)
Abonnieren
Posts (Atom)